听说有人不清楚[时间复杂度]，怪我。看完这篇还不清楚，那么请来怼我！--20210716

发表于 | 分类于

大家好，指北君学习了一段时间的算法，听说有人对时间复杂度还不太清楚，那么今天它来了。

时间复杂度是是怎么定义的？ 又是如何计算出来的？

指北君带你一探究竟！

1 算法与时间复杂度

算法（Algorithm）是求解一个问题需要遵循的，被清楚指定的简单指令的集合。
算法一旦确定，那么下一步就要确定该算法将需要多少时间和空间等资源，如果一个算法需要一两年的时间来完成，那么该算法的用处就不会太大。同样如果该算法需要若干个GB的内存，那么在大部分机器上都无法使用。

一个算法的评价主要从时间复杂度和空间复杂度来考虑。

而时间复杂度是一个函数，定性描述该算法的运行时间，通常用大O符号表示。

常见的时间复杂度有O(1),O(logn),O(n),O(n^2),O(2^n)…等

那么一个算法的时间复杂度如何计算呢，下面接着讲。

2 时间复杂度计算

2.1 第一个时间复杂度计算

首先我们定义算法中的语句执行次数称为语句频度或时间频度为T(n)。即T(n)表示程序的执行次数 。

首先我们看看如下的方法1执行多少次；

1
2
3
4
	public int method1(){
	    System.out.println("java技术指北 等你来"); //执行1次
	    return 0;				      //执行1次
	}

没错，它内部一共执行2次。

那么我们来看下面的方法2执行几次：

1
2
3
4
5
6
7
    public int method2(int n){
        for(int i = 0; i<n ; i++){
         //i = 0 执行1次，i<n 执行n+1次，i++执行n次
            System.out.println("java技术指北 等你来"); //输出语句执行n次
        }
        return 1; //return 执行一次
    }

对，它一共执行了 3n+3 次。

那么对于方法1就有 T(n) = 2;
对于方法2就有 T(n) = 3n + 3;

实际的代码肯定比示例中的代码复杂得多，去统计代码的执行次数显然不可能，所以算法一般使用T(n)的渐进估算值来反映代码的执行速度。而这个估算值我们用”时间复杂度”来表示。

所以针对方法1和方法2，如何根据T(n)估算出时间复杂度
过程如下：

  1. 对于 T(n) = 2 ，由于T(n)是一个常数，那么时间复杂度可以直接估算为 1 。所以T(n) = 2 的时间复杂度为 1。 用标准的时间复杂度函数表示就是 O(1)。
  2. 对于T(n) = 3n + 3 ，随着n值得不断增长，常数3相对于3n来说可以忽略不计。而系数一般也会估算成1。相当于去掉了系数和常数，则该时间复杂度为n。 用时间复杂度函数表示就是O(n)。
  3. 依次推广到如下多项式中： 对于T(n) = 3n^2 + 3n + 3. 随着n值得不断增大，多项式后面的项的增长就远没有n^2的增长大，可以直接舍弃低阶项和常数项，则只保留n的次方数最大的那一项，所以它的时间复杂度就为O(n^3)。

小结一下，以上三个表达式的时间复杂度表示如下

表达式 时间复杂度
T(n) = 2 O(1)
T(n) = 3n + 3 O(n)
T(n) = 3n^2 + 3n + 3 O(n^2)

总结以上规律：

  • T(n)是常数：时间复杂度为O(1)
  • T(n)不是常数：时间复杂度为O(T(n)的最高次项并且去掉最高次项的系数)

2.2 常见循环的复杂度

下面方法1的时间复杂度为 O(1):

1
2
3
4
5
6
7
    //时间复杂度为 O(1)
    public void m1(){
        System.out.println("java技术指北 等你来");
        System.out.println("操千曲而后晓声，观千剑而后识器");
        ...
        System.out.println("java技术指北 非你莫属");
    }

下面方法2的时间复杂度为 O(n):

1
2
3
4
5
6
7
    //时间复杂度为 O(n)    
    public int method2(int n){
        for(int i = 0; i < n ; i++){
            System.out.println("java技术指北 等你来");
        }
        return 1;
    }

下面方法3 时间复杂度为 O(n^2):

1
2
3
4
5
6
7
8
    //时间复杂度为 O(n^2)
    public void method3(int n){
        for(int i = 0; i < n ; i++){
            for(int j = 0 ; j < i ; j ++){
                System.out.println("java技术指北 等你来");
            }
        }
    }

下面方法4的时间复杂度为 O(n^2)：
以下方法4中第一个循环执行Q其时间复杂度为为O(n^2)
第二个循环时间复杂度为O(n)
则整个方法的时间复杂度要舍弃变化小的部分，最终的时间复杂度为O(n^2)

1
2
3
4
5
6
7
8
9
10
11
12
    //时间复杂度为 O(n^2) 
    public int method4(int n){
        for(int i = 0; i < n ; i++){
            for(int j = 0 ; j < i ; j ++){
                System.out.println("java技术指北 等你来");
            }
        }
        for(int i = 0; i < n ; i++){
            System.out.println("java技术指北 等你来");
        }
        return 1;
    }

方法5的时间复杂度依然为O(n):
由于随着n的增大，方法5种执行次数最多的是else后面的循环，所以会取执行次数最多的部分来计算时间复杂度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
    //时间复杂度为O(n)
    public int method5(int n){
        if( n < 100){
            for(int i = 0; i < n ; i++){
                for(int j = 0 ; j < n ; j ++){
                    System.out.println("java技术指北 等你来");
                }
            }
        }else{
            for(int i = 0; i < n ; i++){
                System.out.println("java技术指北 等你来");
            }
        }
        return 1;
    }

2.3 其他时间复杂度计算

分析下面方法6的时间复杂度

1
2
3
4
5
6
7
    public void method6(int n){
        for(int i = 0; i < n ; i++){
            for(int j = 0 ; j < n ; j ++){
                System.out.println("java技术指北 等你来");
            }
        }
    }

方法6执行分析
i=0 输出语句执行 n 次
i=1 输出语句执行 n-1 次
i=2 输出语句执行 n-2 次
…
…
i=n-2 输出语句执行 2 次
i=n-1 输出语句执行 1 次

总执行次数就是
T(n) = n + (n-1) + (n-2) … + 2 + 1
= n(n+1)/2 = 1/2*n^2 = \(\frac{n(n+1)}{2} = \frac{1}{2}n^2 +\frac{1}{2}n = O(n^2)\)

则其时间复杂度为O(n^2)

下面我们在看方法7的时间复杂度

1
2
3
4
5
6
7
    public void method7(int n){
        int i = 1;
		while(i<n)
		{
		    i = i * 2;
		}
    }

执行情况分析：
n = 2 的时候执行1次 即 T(2) = 1
n = 4 的时候执行2次 即 T(4) = 2
n = 8 的时候执行3次 即 T(8) = 3
n = 16 的时候执行4次 即 T(16) = 4

我们发现如下规律
n = 2 的时候有 2^T(2) = 2
n = 4 的时候有 2^T(4) = 4
n = 8 的时候有 2^T(8) = 8
n = 16 的时候有 2^T(16) = 16
n = 32 的时候有 2^T(32) = 32
n = n 的时候有 2^T(n) = n

如果要把T(n)放到等式左边那么 \(T(n) = \log_2n\)
那么时间复杂度就是\(O(log_2n)\)
再去掉底数2 则时间复杂度为\(O(logn)\)

3 时间复杂度排序

我们分析了以上几种简单循环的时间复杂度，那么既然时间复杂度是用来表示算法的执行效率的，我们对一般常见的时间复杂度进行如下排序(由快到慢)。

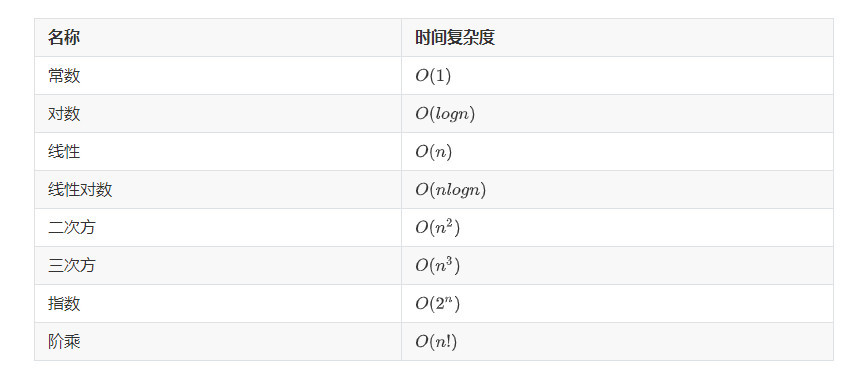
timeComplexitiesOrder.jpg

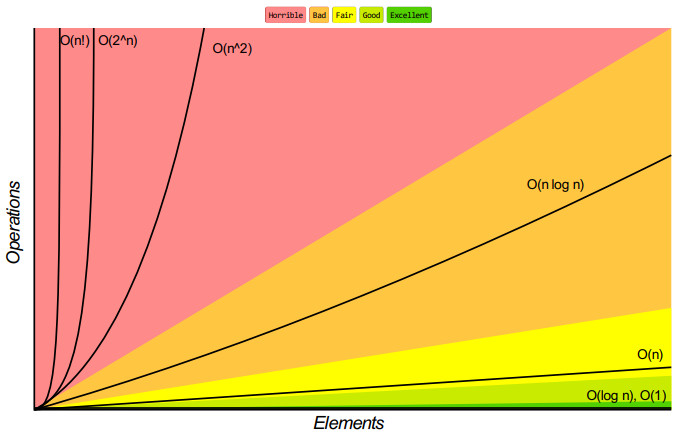
我们再用曲线图看一下时间复杂度。 timeComplexitiesChart.jpg

从图中也可以看出，随着元素变多，指数、阶乘级别的增长是最快的。显而易见其执行效率最低。

4 时间复杂度推算

最后我们计算一下如下递推关系的算法的时间复杂度
T（n）= T(n-1) + n,其中 T(0) = 1，求T(n)的时间复杂度？

我们可以将n-1 带入上面的公式，得到 T(n-1) = T（n-2） + (n-1)
再将T(n-1) 的表达式带入到T(n)的表达式
再依次将n-2 ,n-3…带入到公式中，其演算结果如下。

T（n）= T(n-1) + n
= T（n-2） + (n-1) + n
= T（n-3） +(n-2) + (n-1) + n
……
= T（2） + 3 + ……(n-2) + (n-1) + n
= T（1） + 2 + 3 + ……(n-2) + (n-1) + n
= T（0） + 1 + 2 + 3 + ……(n-2) + (n-1) + n
= 1 + 1 + 2 + 3 + …… + (n-1) +n

\[=\frac{n(n+1)}{2} + 1 = \frac{1}{2}n^2 + \frac{1}{2}n+1 = O(n^2)\]

最终我们得到T(n) 的时间复杂度为O(n^2)

总结

本篇介绍了时间复杂度以及如何计算时间复杂度，相信你已经掌握了吧。如果还有那位小伙伴有疑问，请随时后台@指北君哦！

我是指北君，操千曲而后晓声，观千剑而后识器。感谢各位人才的：点赞、收藏和评论，我们下期更精彩！

Java Geek Tech wechat
欢迎订阅 Java 技术指北，这里分享关于 Java 的一切。